Алгоритм градиентного спуска и его интуиция

Градиентный спуск и его интуитивное понимание

Техническое описание метода градиентного спуска, дополненное графическим представлением алгоритма в работе

1. ВВЕДЕНИЕ НЕКОТОРЫХ КЛЮЧЕВЫХ ОПРЕДЕЛЕНИЙ

В рамках методов оптимизации, и в первом типе алгоритмов, непременно слышали о таком, как градиентный спуск. Это оптимизационный алгоритм первого порядка, так как он требует первого производного, а именно градиента. Оптимизируясь, градиентный спуск стремится минимизировать разницу между «фактическим» результатом и предсказанным результатом модели, измеряемую целевой функцией, а именно функцией стоимости. Градиент, или наклон, определяется как направление линии, проведенной такой функцией (кривой или прямой) в заданной точке этой линии. Итеративно градиентный спуск стремится дифференцировать функцию стоимости в разных точках линии, чтобы определить степень изменения направления в этих точках и, таким образом, сделать шаги в сторону крутого спуска, а именно локального минимума. Как следует из его названия, градиент используется как направление к крутому спуску в поисках локального минимума, где значения параметров функции стоимости, которые оптимизируются, минимизируются и достигают своих наименьших значений.

Градиентный спуск в основном используется (среди прочих) для обучения моделей машинного обучения и моделей глубокого обучения, последние основаны на типе архитектуры нейронной сети. От линейной регрессии и логистической регрессии до нейронных сетей, градиентный спуск стремится вычислить лучшие значения параметров функции. В своей простейшей форме градиентный спуск стремится минимизировать ошибку в нижеприведенной линейной регрессии, вычислив оптимальные значения параметров для независимых переменных. Это,

y = β0 + β1 * X1 + … βk * Xk + Ɛ

где,

• Hugging Face представляет IDEFICS Первоначальная открытая мультимодальная разговорная ИИ с визуальными моделями языка
• Глубокое обучение в распознавании изображений техники и вызовы
• Смотри и учись, маленький робот этот подход искусственного интеллекта обучает роботов универсальному управлению с использованием видеодемонстраций человека.

y – зависимая переменная

k – количество независимых переменных

X – независимая переменная

β – параметр

Ɛ – ошибка

В своей более сложной форме градиентный спуск чаще всего определяется как оптимизатор при обучении модели глубокого обучения, в частности на этапе компиляции. Глубокое обучение основано на взаимосвязанной сети, которая постоянно учится и улучшается, а именно нейронной сети. Вдохновленная человеческим мозгом, нейронная сеть представляет собой высоко сложную сеть, представленную искусственными нейронами, известными как узлы. На верхнем уровне узлы играют важную роль в обработке и анализе данных от узла в предыдущем слое и передаче их другому узлу в следующем слое. В нейронной сети вес, а именно параметры интереса для оптимизации, являются связью между узлами. Они являются связью между входами/признаками и скрытыми слоями, поэтому они представляют важность данного признака для предсказания конечного результата. Нахождение оптимального значения одного веса зависит от значения многих весов. И эта оптимизация происходит одновременно для многих весов, которых в глубокой нейронной сети может быть значительно много, даже миллионы. Здесь градиентный спуск показывает высокую эффективность при большом количестве вычислений, основанных на трех основных слоях нейронной сети: 1) Входной слой 2) Скрытый слой и 3) Выходной слой.

Существует множество статей, которые подробно описывают и расширяют методы глубокого обучения и методы оценки значений параметров функции, а также различия между градиентным спуском и методом наименьших квадратов (OLS), в случае линейной регрессии, например. Поскольку это не является основной темой данной статьи, читателя приглашают к дальнейшему изучению и расширению для лучшего понимания таких методик.

2. ВРЕМЯ ДЛЯ НЕКОТОРОГО ИСЧИСЛЕНИЯ!

Для лучшего понимания градиентного спуска нам нужно расширить определение дифференцируемой функции. Функция, явно ƒ(x), является дифференцируемой, когда производная может быть определена в любой точке кривой линии, полученной этой функцией. Это верно для всех точек в области определения функции ƒ(x). Здесь два понятия подтверждают это определение: производная первого порядка и производная второго порядка. Формула производной первого порядка определяется следующим образом:

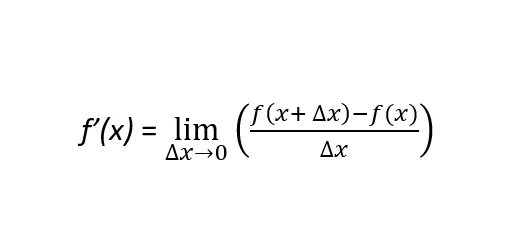
Строго говоря, первая производная функции, обозначаемая как ƒ’(x) или df(x)/dx, является наклоном функции ƒ(x) в заданной точке значения x. Если наклон положительный (отрицательный), это указывает на то, что функция возрастает (убывает) и насколько. Положительный наклон указывает на то, что с увеличением значения x увеличивается и функция ƒ(x). Отрицательный наклон, с другой стороны, указывает на то, что с увеличением значения x уменьшается ƒ(x). Вторая производная – это производная от производной функции ƒ(x). Обозначается как ƒ’’(x) или d2f(x)/dx2, вторая производная указывает на форму функции ƒ(x). А именно, является ли такая функция вогнутой или выпуклой. Математически говоря, (и это важно!!!) вторая производная будет различать относительный максимум от относительного минимума.

где,

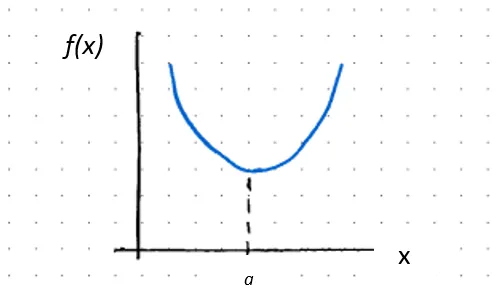
ƒ’’(x) > 0, тогда ƒ(x) вогнута при x = a

и если ƒ’(a) = 0, тогда a – критическая точка, следовательно, относительный минимум

где,

ƒ’’(x) < 0, тогда ƒ(x) вогнута при x = a

и если ƒ’(a) = 0, тогда a – критическая точка, следовательно, относительный максимум

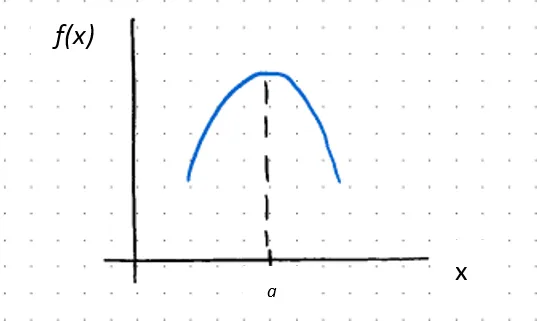
или если вторая производная равна нулю, то либо 1) функция ƒ(x) находится в точке перегиба, известной как точка перегиба, где она меняет свою выпуклость на вогнутость или наоборот, или 2) функция в этой точке неопределена (т.е. непрерывная). В случае первого:

ƒ’’(x) = 0, тогда ƒ(x) находится в точке перегиба при x = 2

Выше было сосредоточено на функции с одной независимой переменной, а именно унитарной функции, y = ƒ(x). В реальном мире будут изучаться и моделироваться многомерные функции, где переменная, изучаемая, зависит от нескольких факторов, это две или более независимых переменных, y = ƒ(x, z). Чтобы измерить влияние изменения независимой переменной x на зависимую переменную y, при сохранении постоянной переменной z, берется частная производная функции по отношению к x. Таким образом, частные производные вычисляют скорость изменения функции стоимости вследствие изменения каждого из их входных данных. Градиентный спуск итеративно вычисляет эти изменения функции стоимости и на каждом шаге обновляет значения параметров таких функций, пока не достигнет минимальной точки, где значения таких параметров оптимизированы, следовательно, функция стоимости минимизирована.

3. АЛГОРИТМ ГРАДИЕНТНОГО СПУСКА В ДЕЙСТВИИ

Чем больше абсолютное значение наклона, тем дальше мы можем сделать шаг, и/или мы можем продолжать делать шаги в сторону наиболее крутого спуска, то есть локального минимума. При приближении к самой низкой/минимальной точке наклон уменьшается, поэтому можно делать более маленькие шаги, пока не достигнется плоская поверхность, где наклон равен нулю (0), ƒ’(x) = 0, это наименьшее значение βi, указанное красной стрелкой на графике ниже. Здесь находится локальный минимум изогнутой линии, и вычисляются оптимальные значения параметров функции.

Таким образом, если функция строго выпуклая (вогнутая), будет только одна критическая точка. Теперь есть случай, когда есть несколько локальных минимумов. В этом случае поиск осуществляется для единственного наименьшего значения, которое функция может достичь. Это известно как глобальный минимум.

Возникают два основных вопроса:

1) В каком направлении делать шаг?

2) Какова должна быть величина шагов?

Давайте кратко подведем итоги того, что мы сказали до сих пор. Градиентный спуск – это алгоритм, который во время обучения модели итеративно корректирует и оптимизирует значения параметров функции, беря частные производные функции по каждому из ее входов на каждом шаге в сторону наиболее крутого спуска, определенного как локальный минимум. Если производная положительна, функция возрастает. Таким образом, шаги должны быть сделаны в противоположном направлении. Градиент указывает, в каком направлении следует сделать шаг. Если градиент большой, то есть большое абсолютное значение наклона, следует делать более крупные шаги в сторону локального минимума. Фактически, градиентный спуск делает все более маленькие шаги в направлении локальных минимумов на каждой итерации, как показано синими стрелками на графике выше.

Какова должна быть величина шага связана с коэффициентом обучения. Это определяет, насколько быстро алгоритм учится/движется в сторону наиболее крутого спуска. При наивысшем градиенте, большем абсолютном значении наклона, алгоритм учится наиболее быстро. По мере приближения к локальному минимуму, шаги становятся меньше. Таким образом, значение коэффициента обучения, как и любого гиперпараметра, устанавливается после проверки разных значений, чтобы функция стоимости уменьшалась на протяжении итераций. Если значение слишком большое, локальный минимум может быть пропущен. Слишком маленький коэффициент обучения может привести к незначительному обновлению весов и незначительному улучшению модели. Если слишком маленький, потребуется время, чтобы достичь сходимости. Сходимость достигается, когда функция стоимости больше не уменьшается. Таким образом, функция стоимости является показателем производительности алгоритма. В многомерном мире функция обозначается следующим образом:

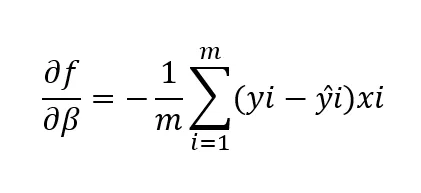
где,

df/dβ – частная производная функции стоимости по параметру β

m – количество точек данных

yi – фактические значения зависимой/целевой переменной для i-ой точки данных

ŷi – предсказанные значения модели зависимой/целевой переменной для i-ой точки данных

xi – представляет i-ый вход, связанный с точкой данных.

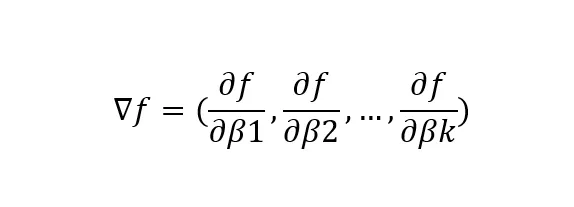
где,

▽f представляет градиентный вектор функции f(x) относительно параметров β

df/dβk представляет частную производную функции f(x) по k-му параметру β

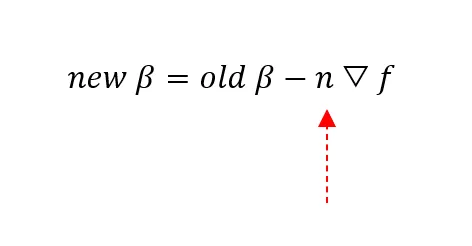
где,

New β представляет текущее значение i-го параметра β

Old β представляет обновленное значение i-го параметра β

n – коэффициент обучения: длина шага, который нужно сделать!

▽f – градиентный вектор, указывающий в направлении наиболее крутого спуска функции f(x) относительно изменений параметров β для минимизации f(x)

4. ОГРАНИЧЕНИЯ ГРАДИЕНТНОГО СПУСКА

Одно из ограничений градиентного спуска связано с одним из указанных выше критериев, где функция должна быть дифференцируемой в каждой точке своей области определения. Когда это не так и алгоритм находит точку, которая не определена (т.е. не непрерывная), то он не работает.

Еще одно ограничение связано с размером шагов, а именно с коэффициентом обучения (n), сделанных в сторону наиболее крутого спуска. Если он слишком большой, вероятно, будет пропущен локальный минимум или вообще не будет достигнута сходимость. Если слишком маленький, потребуется гораздо больше времени для сходимости. Если количество входов большое, это становится еще более проблематичным.

Наконец, градиентный спуск может никогда не найти глобальный минимум. Алгоритм не способен отличить локальный и глобальный минимумы. Он спускается в поисках локального минимума, и как только сходится, он останавливается. Локальный минимум заключит алгоритм в своей собственной долине и не позволит шагу быть достаточно большим для выхода.

5. ВЫВОДЫ

В заключение, градиентный спуск:

1) Является итеративным, оптимизационным алгоритмом первого порядка

2) В каждой итерации обновляются параметры дифференцируемой функции и минимизируется функция стоимости.

3) Таким образом, достигается сходимость к локальному минимуму.

Исходя из ограничений градиентного спуска, есть мотивация исследовать различные и более продвинутые методы градиентного спуска или даже другие типы алгоритмов в области оптимизации, такие как метод второго порядка. Однако это выходит за рамки данной статьи, поэтому я оставлю это в качестве темы для моей следующей статьи 😊

Спасибо за чтение!

Пожалуйста, добавьте любой комментарий, который, по вашему мнению, улучшает знания по данной теме!