Информация и энтропия

Информация и энтропия' - Сжатая версия

Что, почему и как объясняется

Используйте “энтропию” и вы никогда не проиграете дебаты, сказал фон Нейманн Шеннону, потому что никто на самом деле не знает, что такое “энтропия”.

— Уильям Паундстоун

Давайте начнем с немного истории.

В 1948 году математик по имени Клод Шеннон опубликовал статью под названием “Математическая теория связи”, в которой было представлено ключевое понятие в Машинном обучении: энтропия.

• Картографирование пробок Анализ трафика с использованием теории графов
• Исследовательский анализ данных датчиков MEMS
• Моделирование тематического парка Понимание времени ожидания в очереди с помощью R

Хотя энтропия измеряет беспорядок в физике, ее значение меняется в теории информации. Однако оба они измеряют беспорядок или неопределенность.

Давайте погрузимся в представление о “Информации”.

I. Информация Шеннона

Согласно статье, мы можем количественно оценить информацию, которую событие передает, что можно интерпретировать как измерение уровня “удивления”. Это означает, что содержание информации по сути представляет собой степень удивления, содержащегося в событии.

Давайте рассмотрим пример: Представьте, что кто-то говорит вам: “Животные нуждаются в воде для выживания”. Насколько вы удивлены, услышав эту фразу?

Вы не будете удивлены вообще, потому что это хорошо известный и постоянно истинный факт. В таком случае количество удивления равно 0, и, следовательно, передаваемая информация также равна 0.

Но что, если кто-то скажет: “Монета упала орлом”? Ну, это событие (орел) не гарантировано, верно? Всегда есть 50-50 шанс того, что результат может быть как орел, так и решка. Следовательно, услышав этое утверждение, возможно, вызовет определенный уровень удивления. В этом лежит увлекательная корреляция между вероятностью и удивлением. Когда событие абсолютно определено (с вероятностью 1), мера удивления уменьшается (становится 0). Соответственно, по мере уменьшения вероятности – то есть когда событие становится менее вероятным – чувство удивления возрастает. Это обратная связь между вероятностью и удивлением.

Математически,

где p(x) – это вероятность события x.

Мы знаем, что информация – это просто количество удивления. И так как мы пытаемся провести некоторые математические вычисления, мы можем заменить слово “удивление” на “информацию”.

Что, если вы делаете информация = 1/p(x)?

Давайте рассмотрим это на некоторых крайних случаях:

Когда p(x) = 0, информация = 1/0 = ∞ (бесконечность/неопределенность). Этот результат соответствует нашей интуиции: событие, которое считалось невозможным, но все же произошло, приведет к бесконечному или неопределенному удивлению/информации. (Невозможный сценарий) ➟ ✅

Когда p(x) = 1, информация = 1/1 = 1, что противоречит нашему наблюдению. В идеале, мы стремимся к 0 удивления в случае абсолютно вероятного события.

➟ ❌

К счастью, логарифмическая функция приходит на помощь. (В течение этого поста мы будем последовательно использовать логарифм по основанию 2, обозначаемый как log.)

Информация = log (1/p(x)) = log(1) – log(p(x)) = 0 – log(p(x))

Информация = -log(p(x))

Давайте рассмотрим эту новую формулу на некоторых крайних случаях:

когда p(x) = 0, информация = -log(0) = ∞ ➟ ✅

когда p(x) = 1, информация = -log(1) = 0, что действительно желаемый результат, так как абсолютно вероятное событие не должно вызывать удивление/информацию ➟ ✅

Чтобы измерить количество удивления или информации, передаваемой событием, мы можем использовать формулу:

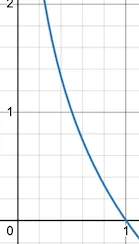
Эта функция -log равна 0 при x = 1 (это означает, что при вероятности равной 1, информация равна 0). При уменьшении x соответствующее значение y резко увеличивается. При x = 0 информация становится бесконечной или неопределенной. Эта кривая точно отражает наше интуитивное понимание информации.

И для серии событий это становится

Что не что иное, как сумма информации о каждом событии. Единица информации – «биты». Вот еще одна интуитивная перспектива:

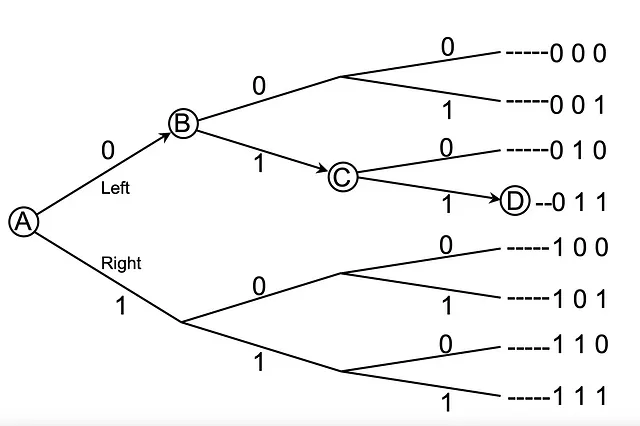
Представьте, что вы находитесь в точке A и хотите достичь точки D. Однако у вас нет представления о маршрутах и нет видимости смежных точек. Кроме того, вы не можете перемещаться назад.

Находясь в точке A, у вас есть два выбора: Влево(0) и Вправо(1). Я отправляю вам один бит, 0, один бит информации, которая помогает вам выбрать из 2 вариантов (второй столбец). По прибытии в точку B я даю вам значение бита 1, всего 2 бита, позволяющих вам выбрать из 2 * 2 = 4 вариантов (третий столбец). Когда вы продвигаетесь к C, я отправляю вам еще одну 1, всего 3 бита. Это помогает вам выбрать из 2 * 2 * 2 = 8 вариантов (последний столбец). И интересно, 1 – это логарифм 2, 2 – логарифм 4, и 3 – логарифм 8.

‘n’ бит информации позволяют нам выбирать из ‘m’ вариантов.

Например, 8 = 2 ³ (где m = 8 представляет собой общее количество возможных результатов, а n = 3 представляет собой количество битов)

В общем,

m = 2ⁿ

Это уравнение для информации (количество полезных битов).

Основная интуиция информационной теории заключается в том, что узнавание о том, что произошло маловероятное событие, является более информативным, чем узнавание о том, что произошло вероятное событие.

— Страница 73, Deep Learning, 2016.

II. Энтропия

Давайте рассмотрим сценарий, когда мы хотим генерировать случайные числа из заданного списка [1, 2, 3, 4] с использованием вероятностного распределения.

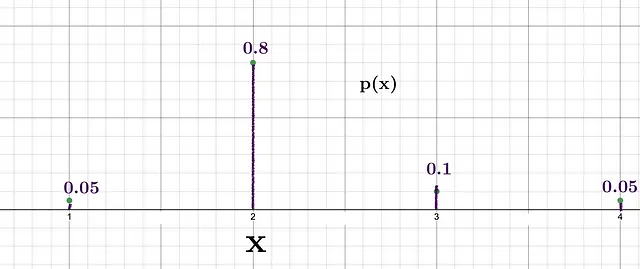
Мы видим, что вероятность получить 2 наибольшая, что означает, что уровень удивления при получении 2 будет относительно ниже по сравнению с удивлением при получении 3, у которого вероятность 0.1. Информация Шеннона для этих двух событий:

• Информация для 2 = -log(0.8) = 0.32 бита
• Информация для 3 = -log(0.1) = 3.32 бита

Обратите внимание, что каждый раз, когда мы генерируем число, полученная информация меняется.

Предположим, что мы выполняем этот процесс генерации 100 раз в соответствии с заданным распределением. Чтобы вычислить общую информацию, нам нужно сложить индивидуальную информацию, полученную в каждом случае.

Количество наблюдений, генерирующих 1 = 0,05 * 100 = 5,

Количество наблюдений, генерирующих 2 = 0,8 * 100 = 80

Количество наблюдений, генерирующих 3 = 0,1 * 100 = 10

Количество наблюдений, генерирующих 4 = 0,05 * 100 = 5

Теперь давайте вычислим общую информацию, передаваемую 100 поколениями.

Информация, полученная при генерации 1 в 5 раз = — log(0,05) * 5 = 21,6 бит

Информация, полученная при генерации 2 в 80 раз = — log(0,8) * 80= 25,8 бит

Информация, полученная при генерации 3 в 10 раз = — log(0,1) * 10= 23,2 бит

Информация, полученная при генерации 4 в 5 раз = — log(0,05) * 5 = 21,6 бит

Общая информация = 92,2 бит

Таким образом, общая информация, передаваемая 100 наблюдениями, составляет 92,2 бит.

Было бы неплохо, если бы мы рассчитали информацию на одно наблюдение (среднюю)?

Средняя информация по данному распределению = 92,2 / 100 (потому что у нас было 100 наблюдений)

Средняя информация = 0,922 бита

ДААА, это величина, которую мы называем ЭНТРОПИЯ.

Здесь ничего сложного нет, это просто среднее (ожидаемое) количество информации, передаваемой вероятностным распределением. Теперь давайте выведем формулу для энтропии.

p(x) × N дает количество вхождений события x при выполнении N общих наблюдений.

Таким образом, окончательное общее уравнение имеет вид

Где H – это энтропия, а E – это ожидание.

Вы можете следить за мной, так как я буду продолжать писать о искусственном интеллекте и математике.

Ссылки

[1] C. E. SHANNON, “Математическая теория связи”, 1948

[2] Josh Stramer, “Энтропия (для науки о данных) Понятно объяснено!!!”, Youtube, 2022

[3] James V Stone, “Теория информации: введение в учебник”, 2018