Как неопределенность принципа ограничивает анализ временных рядов?

Как неопределенность влияет на анализ временных рядов?

Почему мы не можем одновременно извлекать точную информацию о времени и частоте из временного ряда и как вейвлет-анализ может справиться с этим ограничением

1. Введение

Связь между преобразованием Фурье, принципом неопределенности и анализом временных рядов раскрывает захватывающее взаимодействие, которое определяет извлечение одновременной информации о времени и частоте. Чтобы понять эту связь, важно сначала кратко разобраться в том, что такое преобразование Фурье (FT) и принцип неопределенности. Затем мы исследуем вейвлет-преобразование (WT) в качестве многообещающего инструмента для преодоления этого ограничения, раскрывая конкретные временные проявления частоты с достаточной ясностью.

1.1 Преобразование Фурье

Преобразование Фурье (FT) служит математическим мостом между временной и частотной областями функции. FT можно описать следующим образом:

Я не буду вдаваться в подробности этого интеграла, но важная часть заключается в том, что FT преобразует функцию f(x) в другую функцию g(ω) в пространстве частот. Запомните эту информацию, она будет важной. (Чтобы лучше понять преобразование Фурье, я настоятельно рекомендую видео от 3Blue1Brow.)

• Геопространственная инженерия данных пространственный индексирование
• 5 навыков, которыми должны обладать все профессионалы в области маркетингового анализа и науки о данных сегодня
• Проверка данных для приложений PySpark с использованием Pandera

1.2 Принцип неопределенности как следствие преобразования Фурье

В 1927 году физик Вернер Гейзенберг представил, вероятно, одну из самых известных концепций квантовой механики, принцип неопределенности [1]. Этот принцип, по сути, является теоремой о преобразованиях Фурье, когда две функции являются преобразованием Фурье друг друга, вступает в действие принцип неопределенности.

Пока мы на время отступим от его сложной физики, рассмотрим лишь суть: произведение неопределенностей в позиции x и импульсе p ограничено. Это ограничение подчеркивает врожденную границу при измерении этих величин с бесконечной точностью (если вас это интересует, посмотрите это видео).

Это происходит потому, что позиция и импульс являются преобразованием Фурье друг друга! В случае анализа временных рядов аналогом позиции x и импульса p являются временной ряд во временном пространстве t и частотное пространство ω соответственно.

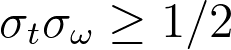
2. Вызов частот с помощью преобразования Фурье во временных рядах

Очень важное применение преобразования Фурье – в анализе временных рядов. Представьте ситуацию, когда нам нужно найти врожденные частоты во временном ряду. Например, подумайте о выявлении преобладающих частот, с которыми люди смотрят определенный контент. Поэтому мы хотим преобразовать f(t) (временной ряд) в g(ω), функцию частот, с помощью преобразования Фурье.

2.1 Пример

Давайте в качестве примера используем набор данных Mauna Loa Weekly Atmospheric CO2 [2].

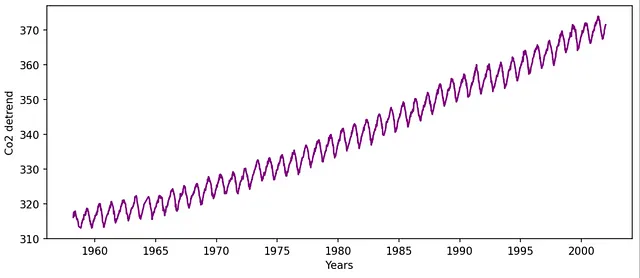
Удаление линейного тренда для удаления поддельных низкочастотных вкладов:

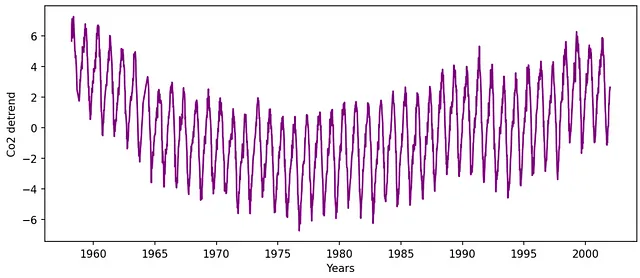
Использование алгоритма быстрого преобразования Фурье (FFT) для вычисления Фурье-преобразования:

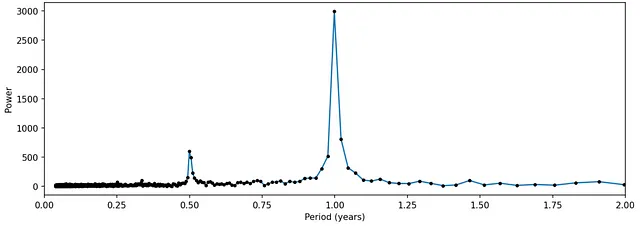
Отсюда можно получить частоту, составляющую ряд, и в данном случае видны два различных пика – один годовой и другой полугодовой. Это визуализация явной сезонности набора данных.

Однако наиболее интересные аспекты происходят, когда во временном ряду происходит возмущение, которое могло бы быть влиянием события или внешней переменной (например, извержения близкого вулкана). Чтобы смоделировать это, мы можем взять тот же ряд, плюс стохастическое синусоидальное слагаемое:

Применение FFT для получения Фурье-преобразования ряда:

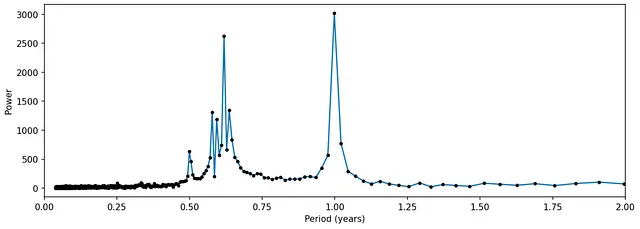
Теперь между 0.5 и 0.75 появляется еще один набор пиков, вызванных возмущением.

2.2 Ограничение

Иногда нам хочется знать, когда произошло возмущение и изменение частоты, или просто временное расположение каждой частоты внутри ряда. В нашей симуляции ряда с и без возмущения ясно, что большая часть влияния происходит в начале ряда. Однако визуальное изучение ряда в сочетании с информацией о Фурье-преобразовании недостаточно, чтобы узнать, где произошло это возмущение. Поэтому нам нужно найти другой инструмент, который поможет нам.

Однако преобразование Фурье (FT) имеет свою цену: оно лишает нас временной информации, как показывает принцип неопределенности, и делает нас невосприимчивыми к тому, когда эти частоты проявляются в ряде. Вот где на сцену выходит принцип неопределенности. Вместо того, чтобы стремиться к бесконечной точности в частоте или времени, мы можем использовать принцип неопределенности, который позволяет нам получать представление о обоих величинах с уменьшенным разрешением, при этом сохраняя баланс.

3. Преобразование Вейвлета как инструмент для балансировки времени и частоты

Преобразование Вейвлета (WT) возникает как акт балансировки разрешения, которое преобразует нашу функцию f(t) в F(t,ω), композицию времени и частоты. Я не буду вдаваться в детали о том, как работает WT, но, чтобы суммировать, процесс преобразования использует ряд различных вейвлетов (сигналов с известной частотой и формой) для согласования временной синхронизации с временным рядом путем скалярных произведений двух функций. Таким образом, можно получить представление о частоте и временном возникновении, но с меньшим разрешением в обоих величинах.

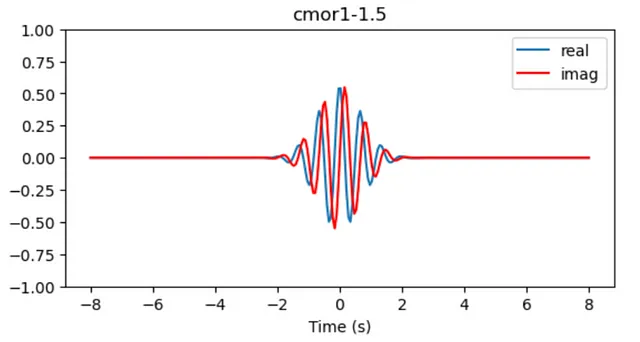
Для визуализации вейвлет-преобразования сигнала обычно используется представление оси x в масштабе времени, оси y в масштабе частоты и цветовой шкалы в виде силы частоты.

Для временного ряда без тренда,

легко видеть, что сезонность повторяется год от года, как и ожидалось при визуальном осмотре. Но огромный пик 1-летней сезонности от Фурье-преобразования стал шире, поэтому наше уверенность в его значении уменьшилась.

Наиболее интересный анализ проводится для симулированного сценария.

Вейвлет-преобразование показывает, что низкочастотное возмущение, наблюдаемое в Фурье-преобразовании, происходит в первые годы ряда, с существенными последствиями после 20-25 лет. Несмотря на потерю разрешения во времени и частоте, новая информация о частотном вхождении ценна и способна дать ответы на различные вопросы.

4. Заключение

Вкратце, принцип неопределенности накладывает фундаментальное ограничение на анализ временных рядов, как показывают ограничения Фурье-преобразования. В то время как Фурье-преобразование эффективно извлекает информацию о частоте из данных временных рядов, оно не дает никакой информации о том, когда эти частоты возникают. Поэтому вейвлет-преобразование является полезным инструментом, который позволяет обменять разрешение во времени и частоте, чтобы получить представление о временном вхождении частотных компонентов с принятием степени неопределенности, присущей принципу.

Благодарности

Это удивительное видео от Артема Кирсанова вдохновило меня на написание этой статьи. Если вы хотите углубиться в эту тему, я также рекомендую посмотреть видео.

Замечания

• Фурье-преобразование (Фурье-спектр) является очень важным не только для квантовой механики и анализа временных рядов. В настоящий момент оно также используется для хранения данных этой статьи в облачном сервисе. Одним из самых известных и используемых алгоритмов в истории является быстрое преобразование Фурье (БПФ), которое лежит в основе практически любого современного метода сжатия данных.
• Для математического описания природы субатомных частиц Фурье-преобразование естественным образом возникает в квантовой механике. Это приводит к фундаментальному изменению в нашем понимании природы, которое несет принцип неопределенности. Измерение положения частицы приводит к потере информации о скорости этой же частицы и наоборот.

Тетрадь для этой статьи доступна здесь.

Ссылки

[1] https://en.wikipedia.org/wiki/Uncertainty_principle

[2] https://www.statsmodels.org/dev/datasets/generated/co2.html (общественное достояние)

[3] Вейвлет-преобразование (Википедия)